Đề thi Toán chuyên Hùng Vương, Gia Lai 2017-2018 (Có đáp án)

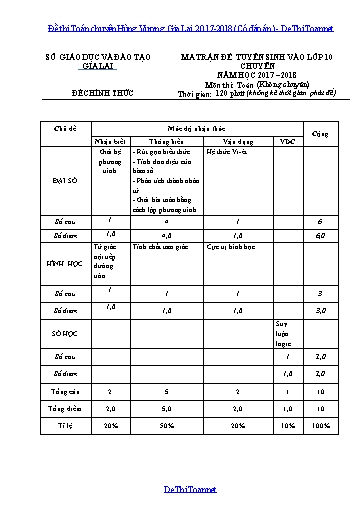
SỞ GIÁO DỤC VÀ ĐÀO TẠO
 GIA LAI
ĐỀ CHÍNH THỨC
MA TRẬN ĐỀ TUYỂN SINH VÀO LỚP 10 CHUYÊN
NĂM HỌC 2017 – 2018
Môn thi: Toán (Không chuyên)
Thời gian: 120 phút (không kể thời gian phát đề)

Chủ đề

Mức độ nhận thức
Cộng
Nhận biết
Thông hiểu
Vận dụng
VDC
ĐẠI SỐ
Giải hệ phương trình
- Rút gọn biểu thức 
- Tính đơn điệu của hàm số
- Phân tích thành nhân tử.
- Giải bài toán bằng cách lập phương trình
Hệ thức Vi-ét
Số câu
1
4
1

6
Số điểm
1,0
4,0
1,0

6,0
HÌNH HỌC
Tứ giác nội tiếp đường tròn
Tính chất tam giác
Cực trị hình học


Số câu
1
1
1

3
Số điểm
1,0
1,0
1,0

3,0
SỐ HỌC



Suy luận logic

Số câu



1
1,0
Số điểm



1,0
1,0
Tổng câu
2
5
2
1
10
Tổng điểm
2,0
5,0
2,0
1,0
10
Tỉ lệ
20%
50%
20%
10%
100%

SỞ GIÁO DỤC VÀ ĐÀO TẠO
GIA LAI
ĐỀ CHÍNH THỨC
KỲ THI TUYỂN SINH VÀO LỚP 10 CHUYÊN
NĂM HỌC 2017 - 2018
Môn thi: Toán (Không chuyên)
Thời gian: 120 phút (không kể thời gian phát đề)

Câu 1: (2,0 điểm)
1. Giải hệ phương trình 
2. Rút gọn biểu thức , với .
Câu 2: (2,0 điểm) 
1. Phân tích thành nhân tử, với là các số không âm.
2. Tìm tất cả giá trị của m để hàm số đồng biến trên .
Câu 3: (2,0 điểm)
1. Một tổ công nhân may lập kế hoạch may 60 bộ quần áo. Khi thực hiện, mỗi ngày tổ này may nhiều hơn kế hoạch 2 bộ nên đã hoàn thành công việc ít hơn kế hoạch 1 ngày. Biết rằng số bộ quần áo may trong mỗi ngày như nhau. Hỏi tổ công nhân may đã lập kế hoạch để hoàn thành công việc trong bao nhiêu ngày?
2. Tìm tất cả giá trị của m để phương trình có hai nghiệm thoả mãn điều kiện .
Câu 4: (3,0 điểm)
Cho đường tròn (O) có AB là một dây cung cố định không qua O. Từ một điểm M bất kì trên cung lớn AB (M không trùng với A và B) kẻ dây cung MN vuông góc với AB tại H. Gọi MQ là đường cao của tam giác AMN (Q thuộc AN).
1. Chứng minh tứ giác AMHQ nội tiếp đường tròn.
2. Gọi I là giao điểm của AB và MQ. Chứng minh tam giác BIM cân.
3. Kẻ MP vuông góc với BN tại P. Xác định vị trí của M sao cho MQ.AN + MP.BN đạt giá trị lớn nhất.
Câu 5: (1,0 điểm)
Tìm các chữ số a, b, c biết .
---------Hết---------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
GIA LAI
ĐỀ CHÍNH THỨC
KỲ THI TUYỂN SINH VÀO LỚP 10 CHUYÊN
NĂM HỌC 2017 - 2018
Môn thi: Toán (không chuyên)
Thời gian làm bài: 120 phút 

HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM
(Hướng dẫn chấm có 02 trang)
Hướng dẫn chung.
Nếu học sinh giải cách khác hướng dẫn chấm nhưng giải đúng thì vẫn được điểm tối đa.
Điểm toàn bài của thí sinh không làm tròn.
Đáp án – Thang điểm.
Câu
Đáp án
Điểm
1
(2 điểm)
1. 
0,25

0,25

0,25
 . Vậy hệ có nghiệm duy nhất .
0,25
2. 
0,25

0,25

0,25

0,25
2
(2 điểm)
1. Ta có = 
0,5

0,25
.
0,25
2. Hàm số đồng biến trên khi 
0,25
, luôn đúng với mọi số m.
0,5
Vậy với mọi số m hàm số đồng biến trên .
0,25
3
(2 điểm)

1. Gọi số ngày tổ may hoàn thành công việc theo kế hoạch là x (ngày) .
0,25
Theo kế hoạch, số bộ quần áo may trong một ngày là (bộ).
Thực tế, số bộ quần áo may được trong một ngày là (bộ).
0,25
Ta được phương trình 
0,25
.
Kết hợp với điều kiện , ta nhận nghiệm x = 6. Vậy theo kế hoạch tổ công nhân may 60 bộ quần áo trong 6 ngày.
0,25
2. Phương trình đã cho có hai nghiệm khi .
0,25
Áp dụng định lý Vi-ét, ta được .
0,25
Ta có .
0,25
. Kết hợp với điều kiện , ta được giá trị cần tìm là .
0,25
4
(3 điểm)
1. Thí sinh chỉ cần trình bày theo một trong hai trường hợp sau

TH1: MA > MB

TH2: MA < MB 

Ta có 
Ta có 
0,5
Suy ra tứ giác AMHQ nội tiếp đường tròn.
Khi đó ta có tứ giác AHMQ nội tiếp đường tròn.
0,5

2. Ta có 
0,25
.
0,25
Suy ra . 
0,25
Do đó tam giác BMI cân tại M.
0,25
3. Ta có 
0,5
.
0,25
Do đó đạt giá trị lớn nhất khi MN lớn nhất, hay MN là đường kính của (O). Khi đó M nằm chính giữa cung AB.
0,25
5
(1 điểm)
Ta có .
0,25
Vì a, b, c là các chữ số khác 0 nên . Do đó .
0,25
Với thì . 
Vậy ,.
0,25
Với thì .
Vậy ,.
0,25
.Hết.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
 GIA LAI
ĐỀ CHÍNH THỨC
MA TRẬN ĐỀ TUYỂN SINH VÀO LỚP 10 CHUYÊN
NĂM HỌC 2017 – 2018
Môn thi: Toán (chuyên)
Thời gian: 150 phút (không kể thời gian phát đề)

Chủ đề

Mức độ nhận thức
Cộng
Nhận biết
Thông hiểu
Vận dụng
Vận dụng cao
ĐẠI SỐ

Rút gọn biểu thức

- Phương trình bậc hai
- Cực trị đại số
- Số chính phương
Bất đẳng thức


Số câu

1
3
1
5
Số điểm

1,0
3,0
1,0
5,0
HÌNH HỌC

Vị trí tương đối của hai đường thẳng
Tam giác đồng dạng
Cực trị hình học

Số câu

1
1
1
3
Số điểm

1,0
1,0
1,0
3,0
SỐ HỌC

- Tính chất chia hết
- Phương trình bậc hai



Số câu

2


2
Số điểm

2,0


2,0
Tổng câu

4
4
2
10
Tổng điểm

4,0
4,0
2,0
10
Tỉ lệ

40%
40%
20%
100%

SỞ GIÁO DỤC VÀ ĐÀO TẠO
GIA LAI
ĐỀ CHÍNH THỨC
KỲ THI TUYỂN SINH VÀO LỚP 10 CHUYÊN
NĂM HỌC 2017 - 2018
Môn thi: Toán (Chuyên)
Thời gian: 150 phút (không kể thời gian phát đề)

Câu 1: (2,0 điểm)
1. Rút gọn biểu thức, với .
2. Tìm tất cả các số nguyên n để biểu thức nhận giá trị nguyên.
Câu 2: (2,0 điểm) 
1. Tìm tất cả các số tự nhiên sao cho là một số chính phương.
2. Cho hai phương trình và , với . Gọi và lần lượt là hai nghiệm lớn của hai phương trình. Chứng minh .
Câu 3: (2,0 điểm)
1. Tìm giá trị của tham số m để phương trình có hai nghiệm là độ dài hai cạnh của một tam giác vuông, biết độ dài cạnh còn lại là 5.
2. Giải hệ phương trình 
Câu 4: (3,0 điểm)
Cho đường tròn (O) đường kính AB = 2R và một điểm M di động trên nửa đường tròn (M không trùng với A và B). Gọi (I) là đường tròn tiếp xúc trong với (O) tại M, tiếp xúc với AB tại N, cắt AM tại C, cắt BM tại D. 
1. Chứng minh CD // AB.
2. Gọi E là giao điểm thứ hai của (O) với đường thẳng MN. Chứng minh .
3. Gọi P, Q lần lượt là giao điểm của CN với BE, DN với AE. Tìm vị trí của M để diện tích tam giác NPQ đạt giá trị lớn nhất.
Câu 5: (1,0 điểm)
Cho ba số thoả mãn điều kiện và . Chứng minh rằng 
.
SỞ GIÁO DỤC VÀ ĐÀO TẠO
GIA LAI
ĐỀ CHÍNH THỨC
KỲ THI TUYỂN SINH VÀO LỚP 10 CHUYÊN
NĂM HỌC 2017 - 2018
Môn thi: Toán (chuyên)
Thời gian làm bài: 150 phút 

HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM
(Hướng dẫn chấm có 03 trang)
Hướng dẫn chung.
Nếu học sinh giải cách khác hướng dẫn chấm nhưng giải đúng thì vẫn được điểm tối đa.
Điểm toàn bài của thí sinh không làm tròn.
Đáp án – Thang điểm.
Câu
Đáp án
Điểm
1
(2 điểm)
1. 
0,25

0,25

0,25

0,25
2. Ta có 
0,25
Vìnguyên nênnguyên. Suy ra 
0,25
Do đó 
0,25
Thử lại, ta nhận các giá trị nguyên của n là .
0,25
2
(2 điểm)
1. Giả sử là một số chính phương. 
Suy ra có số tự nhiên k sao cho 
0,25

0,25
Do và nên có các trường hợp sau

53
-3
159
-1

3
-53
1
-159

40
-16
92
-68

25
25
79
79

0,25
Vậy có hai giá trị cần tìm là ; .
0,25
2. Vì nên hai phương trình đã cho đều có hai nghiệm trái dấu.
Do đó và là hai số dương.
0,25
Ta có .
0,25
Nên .
0,25
Do đó . Dấu bằng xảy ra khi .
0,25
3
(2 điểm)

1. Ta có 
0,25
Nên phương trình đã cho có hai nghiệm là . Ta xét hai trường hợp sau
0,25
TH1: và 3 là độ dài hai cạnh góc vuông. Khi đó .
0,25
TH2: 5 và 3 là độ dài hai cạnh góc vuông. 
Khi đó .
Vậy giá trị cần tìm là .
0,25
2. Điều kiện 
0,25
Ta có: (do )
0,25
Do đó .
0,25
Kết hợp với điều kiện , ta được nghiệm của hệ phương trình là =.
0,25
4
(3 điểm)

1. Ta có (I) tiếp xúc trong với (O) nên OM qua I; nên CD là đường kính của (I).
0,25
(do cân tại I)
0,25
(do cân tại O)
0,25
Nên . Suy ra CD // AB.
0,25
2. + EM là đường kính của (O) thì ta có điều cần chứng minh.
+ EM không là đường kính của (O): Kẻ EF là đường kính của (O).
Ta có 
0,25
Hai tam giác vuông EON và EMF có góc E chung nên đồng dạng với nhau
0,25
Suy ra 
0,25
Do đó .
0,25
3. Tam giác ANQ vuông cân tại Q nên NQ = AQ
Tứ giác EPNQ là hình chữ nhật nên NP = EQ
0,25

0,25
 không đổi.
0,25
 đạt giá trị lớn nhất bằng , đạt được khi , hay tam giác NPQ vuông cân tại N. Khi đó M trùng với F, hay M là điểm chính giữa cung AB.

0,25
5
(1 điểm)
Ta có 
= 
0,25
Vì nên 
Suy ra 
0,25
Do đó 
0,25
Vậy . Dấu bằng xảy ra khi và các hoán vị.
0,25

------Hết------
SỞ GIÁO DỤC VÀ ĐÀO TẠO
 GIA LAI
ĐỀ CHÍNH THỨC
MA TRẬN ĐỀ TUYỂN SINH VÀO LỚP 10 CHUYÊN
NĂM HỌC 2017 – 2018
Môn thi: Toán (Chuyên Tin học)
Thời gian: 150 phút (không kể thời gian phát đề)
Chủ đề
Mức độ nhận thức
Cộng
Nhận biết
Thông hiểu
Vận dụng
VDC
ĐẠI SỐ


- Rút gọn biểu thức 

- Hệ thức Vi-ét
- Tính giá trị của biểu thức
- Giải hệ phương trình
- Parabol 



Số câu

1
4

5
Số điểm

 1,0
 4,0

 5,0
HÌNH HỌC

- Góc với đường tròn.
- Hệ thức lượng trong tam giác vuông.
- Chứng minh bất đẳng thức lượng giác trong tam giác


Số câu

2
1

3
Số điểm

 2,0
 1,0

 3,0
SỐ HỌC

Tìm số tự nhiên thỏa mãn điều kiện cho trước

Suy luận logic

Số câu

1

1
2
Số điểm

 1,0

 1,0
 2,0
Tổng câu

4
5
1
10
Tổng điểm

 4,0
 5,0
 1,0
 10
Tỉ lệ

40%
50%
10%
100%

SỞ GIÁO DỤC VÀ ĐÀO TẠO
 GIA LAI
 ĐỀ CHÍNH THỨC
KỲ THI TUYỂN SINH VÀO LỚP 10 CHUYÊN
NĂM HỌC 2017 – 2018
Môn thi: Toán (Chuyên Tin học)
Thời gian: 150 phút (không kể thời gian phát đề)

Câu 1 (2,0 điểm). 
 a) Rút gọn biểu thức 
 b) Không sử dụng máy tính cầm tay, tính giá trị của biểu thức 
với .
Câu 2 (2,0 điểm). 
 a) Cho phương trình , với m là tham số. Tìm m để phương trình có hai nghiệm , thỏa mãn hệ thức .
 b) Trong mặt phẳng tọa độ Oxy, cho Parabol và điểm Tìm điểm M thuộc (P) sao cho đoạn thẳng AM có độ dài nhỏ nhất.
Câu 3 (2,0 điểm).
 a) Tìm tất cả các số tự nhiên để là một số tự nhiên.
 b) Giải hệ phương trình 
Câu 4 (3,0 điểm). 
 Cho tam giác ABC nhọn có các đường cao AD, BE, CK cắt nhau tại H 
. Lấy điểm đối xứng với H qua BC. Chứng minh rằng:
 a) Tứ giác nội tiếp đường tròn.
 b) 
 c) với 
Câu 5 (1,0 điểm). 
 Lớp 9A1 có 36 học sinh đăng ký dự thi vào các lớp chuyên Toán, chuyên Lý, chuyên Tin của trường THPT chuyên Nguyễn Bỉnh Khiêm (mỗi học sinh có thể đăng ký dự thi vào một hoặc nhiều lớp). Trong đó, không có học sinh nào chỉ chọn thi vào lớp Lý; không có học sinh nào chỉ chọn thi vào lớp Tin; số học sinh chọn thi vào cả hai lớp Toán và Lý bằng số học sinh chỉ chọn thi vào lớp Toán; có 8 học sinh chọn thi vào cả hai lớp Toán và Tin; số học sinh chọn thi vào cả hai lớp Lý và Tin gấp 4 lần số học sinh thi vào cả ba lớp Toán, Lý, Tin; có ít nhất 6 học sinh chọn thi vào cả 3 lớp Toán, Lý, Tin; có ít nhất 1 học sinh chọn thi cả hai lớp Toán và Lý (không th